GCSE AQA Physics - Forces

Finish Sign Up

Contents

Energy
Electricity
Particle Model of Matter
Atomic Structure
Forces
Waves
Magnetism & Electromagnetism
Space Physics

Forces in Action

Friction

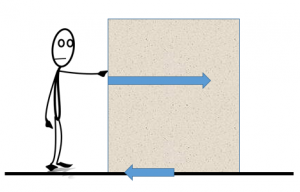
Friction is a force that occurs between two surfaces which are in contact and trying to move past each other. Friction acts in the opposite direction to the motion. Energy used against friction is transformed into heat. The temperature of the object and surface will increase.

Forces in Action, figure 1

Work Done

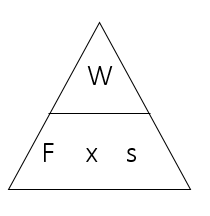
Work done is a measurement of how much energy is required to move an object. It can be calculated using the equation (you DO need to remember this equation for your exam):

W = Fs

W = work done (J)

F = force (N)

s = distance (m)

Forces in Action, figure 1

Worked Example

A race up Ben Nevis starts in a car park 50m above sea level. The top of Ben Nevis is 1344m. Chris weighs 600N and Alison weighs 400N. Calculate the work done by each of them during the race.

  1. Distance climbed = 1294m
  2. Chris: work done = 600 x 1294 = 776,400 J
  3. Alison: work done = 400 x 1294 = 517,600 J
  4. Chris needs more energy for the climb because he weighs more

Elasticity

  1. A force can cause an object to change shape
  2. Elastic materials store Elastic Potential Energy
  3. The EPE is released when the object springs back to its normal shape

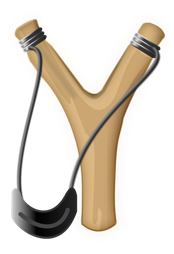
For example, in a catapult

Forces in Action, figure 1

  1. Work done/energy used to stretch catapult
  2. EPE stored in the catapult while it is stretched
  3. EPE released (transformed into Kinetic Energy) when the catapult is released

Or, in a squash ball

Forces in Action, figure 2

  1. Work done/energy used to squash ball
  2. EPE stored in the ball while it is squashed
  3. EPE released (transformed into Kinetic Energy) when the ball is released

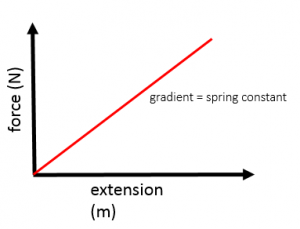
Hooke’s Law

The extension of an elastic object is proportional to the force acting on it.

This can be represented by the equation (you DO need to remember this equation for your exam):

  1. F = k x e
  2. F = force (N)
  3. k = spring constant (N/m)
  4. e = extension (m)

Forces in Action, figure 1

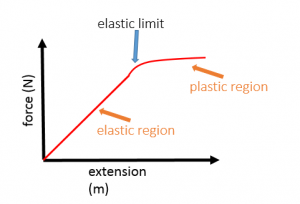
  1. The extension of an elastic object is proportional to the force acting on it until it reaches its elastic limit (limit of proportionality)
  2. After the elastic limit, the object no longer returns to its original shape

Forces in Action, figure 2

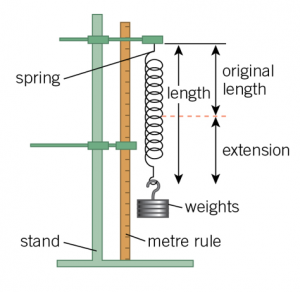
Required Practical – Elasticity

You need to be familiar with the practical method to investigate the relationship between force and extension (Hooke’s law)

Forces in Action, figure 1

Using an elastic material, such as a spring, add masses to the spring and measure the extension with each mass added.

Plotting a graph of force and extension should produce a directly proportional line as shown in the Hooke’s law section above. The gradient of the line is equal to the spring constant of the spring used in the experiment.

Possible causes of error in the experiment include:

  1. Inaccurate measurement of the length or extension due to human error
  2. Stretching the spring past its elastic limit, at which point the relationship between force and extension is no longer proportional and the spring does not return to its original size when the masses are removed

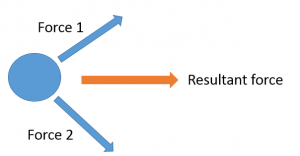
Vector Diagrams

The resultant force on an object is the sum of all the forces acting on an object. If the forces acting on the object are not all acting on the same line, vector diagrams can be used to find the resultant force.

Forces in Action, figure 1

Vector diagrams are drawn to scale. The length of the arrow equals the size of the force (e.g. 2cm = 2N).

Forces in Action, figure 2Draw first force to scale.

Forces in Action, figure 3

Draw second force at the end of the other (using the same scale and at the correct angle)

Forces in Action, figure 4

The resultant force is shown by the line from the starting point to the ending point of your diagram

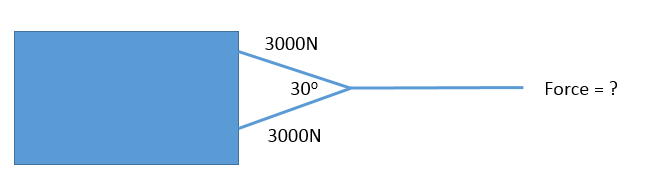
Worked Example

A tow rope is attached to a car at two points 1m apart at 35o to each other. If the pull on each attachment is 3000N, what is the force on the main tow rope?

Forces in Action, figure 5

Choose appropriate scale (e.g. 1cm = 1000N)

Forces in Action, figure 6

Draw first force to scale (3cm = 3000N)

Forces in Action, figure 7

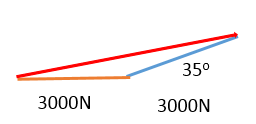
Draw second force at the end of the previous force (at 35o)

Forces in Action, figure 8

Measure resultant line (5.7cm)

Resultant force = 5700N

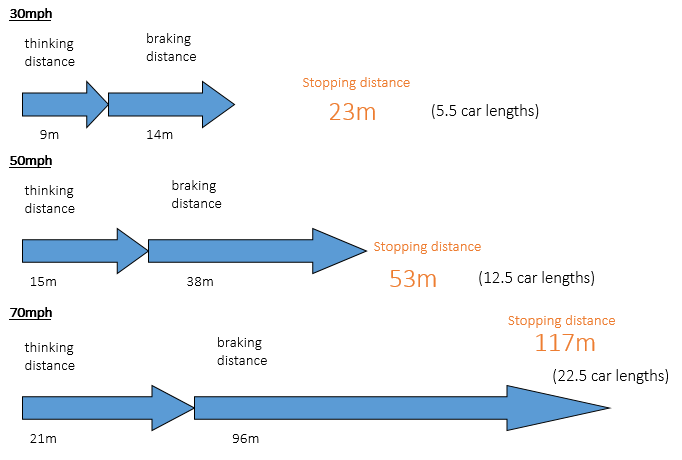
Stopping Distances

Vehicles do not stop instantly. During the time they take to stop, they are still travelling. This distance travelled is known as the stopping distance.

The stopping distance is made up of the thinking distance and the braking distance:

  1. Thinking Distance - The distance travelled in the time it takes the driver to react
  2. Braking Distance - The distance travelled after the brakes have been pressed
  3. Stopping Distance = Thinking distance + braking distance

Forces in Action, figure 1

Factors affecting thinking distance:

  1. Alcohol/Drugs
  2. Tiredness
  3. Age
  4. Speed
  5. Distractions may prevent the driver from stopping as quickly but have not affected his/her reaction time directly

Factors affecting braking distance:

  1. Brake condition
  2. Surface
  3. Tyres
  4. Weather – ice/rain
  5. Speed

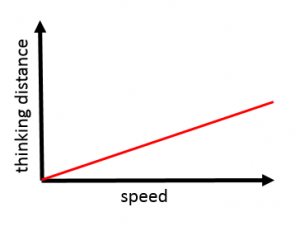
Thinking distance increases in a linear relationship with speed. Thinking distance = speed x time

Forces in Action, figure 2

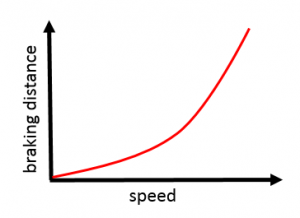
Braking distance increases in a squared relationship with speed. If the speed doubles, the braking distance increases 4 times

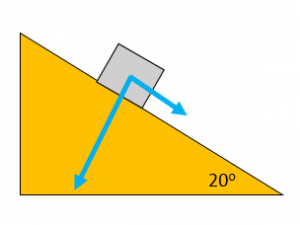
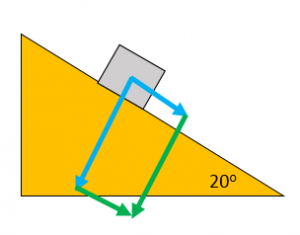
Forces in Action, figure 3

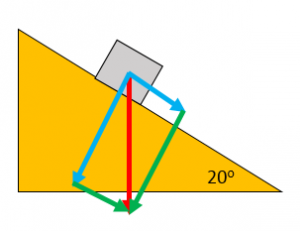
Resolving Forces

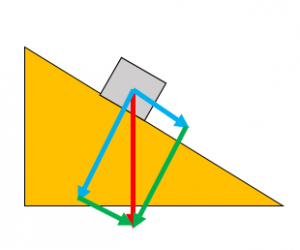
A force acting at an angle can be resolved into two perpendicular forces. Draw a scale diagram, with sides perpendicular to each other and with the original force as the diagonal. If drawn to scale, the sides of the rectangle can be measured to find the size of the force.

Forces in Action, figure 1

Worked Example

A car of weight 10kN is parked on an uphill road. The road is inclined at an angle of 20o. Find the component of the car’s weight that acts down the slope.

Forces in Action, figure 2Draw scale diagram

Forces in Action, figure 3

Complete rectangle with original force as the diagonal

Forces in Action, figure 4

Measure the component down the slope

Component down the slope = 3kN

A man pushes a car with a force of 550N for 12m. How much work was done?
Your answer should include: 6600J / 6600
Explanation: 6600J
A child pulled a toy train across a room with a force of 6N. The child pulls the toy a distance of 4m. How much work does the child do?
Your answer should include: 24J / 24
Explanation: 24J
A pupil investigates Hooke’s law for a spring. When a mass of 100g is hung on the spring, the total length of the spring is 12cm. When a 300g mass is hung on it, the total length of the spring is 16cm. How long will the spring be when 200g is hung on it?
Your answer should include: 14cm / 14
Explanation: 14cm
What is the unstretched length of the spring in the previous question?
Your answer should include: 10cm / 10
Explanation: 10cm
< Motion
Newton's Laws of Motion >
Adapt