Analyzing Circuits

In the last couple of lessons, we have learned about current, potential difference (voltage), and resistance in series and parallel circuits. Students tend to find circuits difficult when these three things are combined, so we will work through some examples in this lesson to help you understand it better.

Any circuit problem can be solved by using a combination of Ohm's law, the current laws, and the voltage laws.

Ohm's law:

voltage = current x resistance

Current laws:

Current is constant in a series circuit.

Current divides down the branches of a parallel circuit.

Voltage laws:

Voltage is shared between components in a series circuit.

Each branch of a parallel circuit receives the same voltage as the power supply.

Worked Examples

Worked Example 1

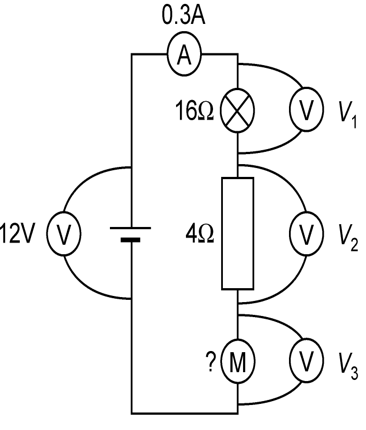
Calculate the voltmeter readings and the resistance of the motor.

Steps to answer this question:

1. Work out whether you are dealing with a series or parallel circuit – in this case, we have a SERIES circuit (the voltmeters don't count as part of the circuit).
2. Voltage 1: We want to use the equation V=IR.
3. In a series circuit, the current is the same everywhere in the circuit, so we know that the current flowing through the bulb is 0.3A.
4. The resistance of the bulb is labeled as 16Ω.
5. V = IR = 0.3 x 16 = 8V.
6. Voltage 2: We want to use the equation V=IR.
7. In a series circuit, the current is the same everywhere in the circuit, so we know that the current flowing through the resistor is 0.3A.
8. The resistance of the resistor is labeled as 4Ω.
9. V = IR = 0.3 x 4 = 1.2V.
10. Voltage 3: We want to use the equation V=IR, but we do not have enough information to use it for this voltmeter – we know the current, but the resistance has not been labeled.
11. At this stage, DON'T PANIC! If we can't use the equation, there must be another way.
12. The voltage law for series circuits says that the voltage supplied by the battery will be shared out between the components. Because we know the voltages of the other two components (and the power supply), we can work out V3.
13. V(battery) = V1 + V2 + V3
14. 12 = 8 + 1.2 + V3
15. V3 = 2.8V
16. Resistance of motor:
17. Rearrange V = IR to R = V/I.
18. R = 2.8/0.3 = 9.33 Ω

Don't panic and work your way through Ohm's law and the current and voltage laws until you have all the information you need.

Worked Example 2

In the circuit shown, the potential difference across the 4Ω resistor is 8V.

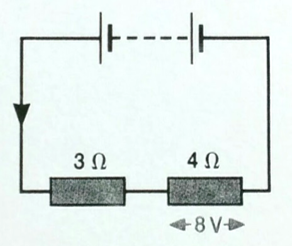
What is the current through the 4 Ω resistor?

Rearrange the equation V=IR to I=V/R.

I = 8/4 = 2A.

What is the current through the 3 Ω resistor?

We do not know the voltage across the 3 Ω resistor, so we cannot use the equation.

We do know that this is a series circuit, and in a series circuit, current is the same everywhere in the circuit.

As we have just calculated in part (a), the current through the other resistor is 2A; therefore, the current through this resistor (and anywhere else in the circuit) is 2A.

What is the p.d. across the 3 Ω resistor?

Use the equation V=IR.

V = IR = 2 x 3 = 6V.

What is the p.d. of the battery?

We do not know the resistance of the battery, so we cannot use the equation.

We do know that this is a series circuit, and in a series circuit, the potential difference (voltage) of the power supply is shared between the components.

As we know the voltages across each resistor, we can simply add those together.

V(battery) = 6 + 8 = 14V.

Remember:

Ohm's law:

voltage = current x resistance

Current laws:

Current is constant in a series circuit.

Current divides down the branches of a parallel circuit.

Voltage laws:

Voltage is shared between components in a series circuit.

Each branch of a parallel circuit receives the same voltage as the power supply.